I've created a comprehensive and complete WinDbg cheat sheet of the most general and useful extensions/commands which you'll be using regularly. I've added a few data structures to the list too. The list is organised by category, according to the different areas of debugging such as Memory or I/O.
Download Link (OneDrive) - https://onedrive.live.com/?cid=7101A9E8FE03DB78&id=7101A9E8FE03DB78!105
If there are any suggestions or corrections to be made, then please leave a comment in the comments section. Additionally, I've been attempting to convert my blog posts into a .DOC format which can be printed, unfortunately I haven't added any images to conserve space and ink. However, I have tried to construct the blog posts so you know which row or column to check; dd commands with the IAT/EAT post for example.
Friday 27 June 2014
Wednesday 18 June 2014
List of Reverse Engineering and Debugging Tools
I may have created a small list of tools before, however, I would like to expand this list and provide some better descriptions for each of the tools listed. These tools are either completely free or have a limited free version which provides enough functionality for those like myself, who aren't professional security researchers, escalation engineers or get paid for doing reverse engineering/debugging. These tools can and are used by professionals and enthusiasts alike. If you have any recommendations then please add a link to the comments section.
WinDbg - Reverse Engineering/Debugging
This tool is my most favorite, it provides complete functionality for enthusiasts and is for free. There is a wide range of extension and commands for viewing data structures, memory addresses and call stacks. It can be used for both reverse engineering and debugging BSODs (Blue Screens of Death).
There is good documentation for WinDbg for finding hidden rootkits, examining data structures and looking at raw memory. Most of this information has been used in my blog for writing tutorials and adding my own information to. It can be used for static analysis and real-time analysis.
Link - Windows Driver Kit (WDK) and Debugging Tools for Windows (WinDbg)
OllyDbg - Reverse Engineering (User-Mode)
OllyDbg is a great tool for reverse engineering user-mode programs. This is a another standard tool if you wish to examine malware or would like to learn the PE structure. This tool is for free, and again is there is great documentation for learning how to use it. Please check the Blogroll section for such blogs.
The data structure being viewed is the _PEB data structure, which is stored at offset 0x30 in the FS register for x86 systems. It is primarily used for static analysis.
Link - OllyDbg v.1.10
IDA Pro - Free Version
This tool is used for reverse engineering, and widely used by professionals to my knowledge. This is a very powerful tool, and be used to examine libraries in the IAT and EAT, look at strings stored in memory and assembly instructions. There are tutorials available on their website.
Link - IDA: About
Analyze It!
This tool is great for displaying information about a specific binary file (static analysis).
I could only find the program hosted on Softpedia, but I'm sure that there wasn't any other programs bundled with the installation package.
Link - Analyze It! Free Download (Softpedia)
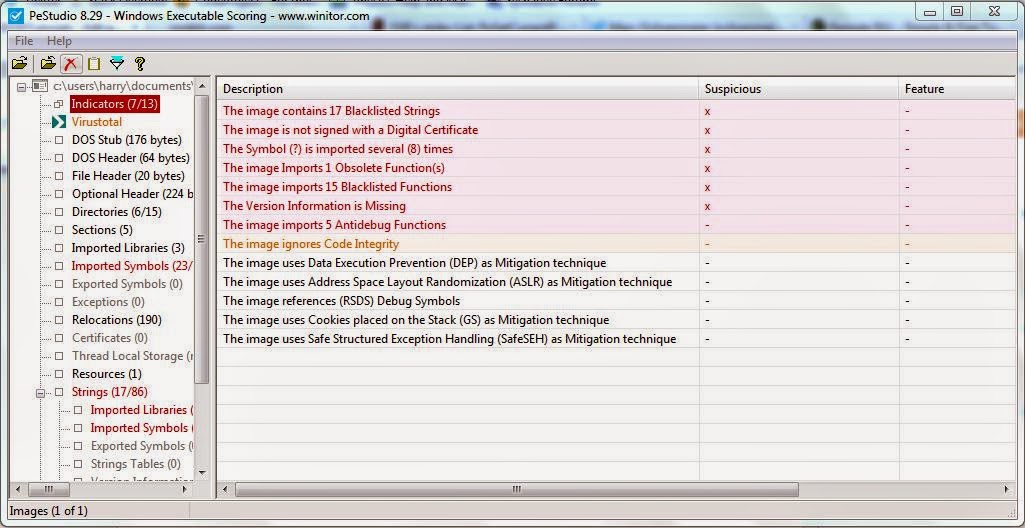
PeStudio
This is tool provides the same features as the other program, but with a simpler and cleaner UI and is easier to use in my opinion. It also has VirusTotal integration.
Link - PeStudio
Twitter -@ochsenmeier (Developer + Updates)
WinDbg - Reverse Engineering/Debugging
This tool is my most favorite, it provides complete functionality for enthusiasts and is for free. There is a wide range of extension and commands for viewing data structures, memory addresses and call stacks. It can be used for both reverse engineering and debugging BSODs (Blue Screens of Death).
There is good documentation for WinDbg for finding hidden rootkits, examining data structures and looking at raw memory. Most of this information has been used in my blog for writing tutorials and adding my own information to. It can be used for static analysis and real-time analysis.
Link - Windows Driver Kit (WDK) and Debugging Tools for Windows (WinDbg)
OllyDbg - Reverse Engineering (User-Mode)
OllyDbg is a great tool for reverse engineering user-mode programs. This is a another standard tool if you wish to examine malware or would like to learn the PE structure. This tool is for free, and again is there is great documentation for learning how to use it. Please check the Blogroll section for such blogs.
The data structure being viewed is the _PEB data structure, which is stored at offset 0x30 in the FS register for x86 systems. It is primarily used for static analysis.
Link - OllyDbg v.1.10
IDA Pro - Free Version
This tool is used for reverse engineering, and widely used by professionals to my knowledge. This is a very powerful tool, and be used to examine libraries in the IAT and EAT, look at strings stored in memory and assembly instructions. There are tutorials available on their website.
Link - IDA: About
Analyze It!
This tool is great for displaying information about a specific binary file (static analysis).
I could only find the program hosted on Softpedia, but I'm sure that there wasn't any other programs bundled with the installation package.
Link - Analyze It! Free Download (Softpedia)
PeStudio
This is tool provides the same features as the other program, but with a simpler and cleaner UI and is easier to use in my opinion. It also has VirusTotal integration.
Link - PeStudio
Twitter -
Hook Analyzer
The program enables you to hook to a certain active process, and then pull information from that process. It only works with Ring 3 (User-Mode) processes to my knowledge.
PE Bear
PE Bear is another static analysis tool for examining PE files, you can view file signatures and view packers which have been used.
Link -PE Bear Blog
WinHex
WinHex can be used for examining the hexadecimal format of files.
Process Explorer
Process Explorer is a Microsoft produced tool, which can be used for finding general information about active processes. It has Virus Total integration.
Sunday 15 June 2014
Computational Number Theory - Pseudo Random Numbers
Computers are increasingly being used to solve mathematical problems, and are becoming more prominent in solving problems in Number Theory and Graph Theory, as well as, fields of Physics and Biology. However, computers have been used to create seemingly random numbers for either games or security purposes; these seemingly random numbers are called Pseudo-Random. They may seem random but in fact they aren't random at all.
To illustrate the difference between a true random number and a pseudo random number, look a look at the two images I've taken from Bo Allen's blog:
The difference is very obvious and thus highlights the key differences between a true random generator and a pseudo random number generator. A pseudo random number generator uses a mathematical algorithm, which is able to produce seemingly random numbers. A true random number generator uses methods which can't be predicted, and therefore are truly random. The randomness of numbers is important for encryption purposes and cryptography.
The true random number generators are hardware based, and most use the physics of Quantum Mechanics and it's probabilistic nature, like the quantization of electromagnetism which lead to discovery of photons and the Photoelectric effect. A pseudo random generator uses a software based mathematical algorithm to generate these random numbers.
A list of random number generators can be found here.
To illustrate the difference between a true random number and a pseudo random number, look a look at the two images I've taken from Bo Allen's blog:
 |
| True Random Number |
 |
| Pseudo Random Number |
The true random number generators are hardware based, and most use the physics of Quantum Mechanics and it's probabilistic nature, like the quantization of electromagnetism which lead to discovery of photons and the Photoelectric effect. A pseudo random generator uses a software based mathematical algorithm to generate these random numbers.
A list of random number generators can be found here.
Saturday 7 June 2014
Data Structures - Red and Black Trees
Before explaining the concept of Red and Black Trees and some of the algorithm analysis related to Red and Black Trees. It's best to have a understanding of some basic Graph Theory, such as what is a tree and the colouring nodes (or vertices). Graph Theory is my favorite area of Mathematics, and has many applications in Computer Science and other subjects. Graph Theory is a very visual form of Mathematics, much like Geometry, and for those who enjoy those types of Mathematics may also enjoy Graph Theory.
A graph G is a ordered pair (V,E), with V being the graph's set of vertices and E being the the graph's set of edges which connect each vertex. Most graphs will have this basic structure, and it's the connections within the vertices which give graph their interesting properties. Hypergraphs are very interesting type of graph in my opinion, and sit between the boundary of Set Theory and Graph Theory. I may talk about more in the future.
 |
| Hypergraph |
 |
| Tree T(9,8) |
A graph is simple if it contains no multiple edges between any two adjacent vertices, or loops (edges which loop onto the same vertex). A graph contains a cycle if there exists a path between at least two vertices within the graph, and the starting and ending vertex are the same. A cycle has no repeated edges or loops. A graph is connected if there exists a path between any two vertices. There is much more to the definitions which I have just given, however, the definitions are suffice for the topic which I'm going to explore.
There is one last Graph Theoretic definition which we must understand before we should learn about Red and Black Trees, and that is the concept of Chromatic Graph Theory, which looks at the idea of giving vertices, edges and faces within a graph distinct colours or groups of colours with certain rules to other vertices and edges within the same graph. A very famous problem was the Four-Colour Theorm.
With Red-Black Trees, the graphs use Vertex Colouring, which is as the name suggests, the colouring of vertices with a certain colour. If no two vertices connected by the same edge i.e any two vertices which are adjacent; do not have the same vertex colour, then the colouring within the graph is proper vertex colouring, which is simply called colouring. However, please bear in mind, that in this context, colouring simply refers to giving each node within the tree a colour: Red or Black. The Chromatic Polynomial can be used to calculate the possible number of proper vertex colourings for a graph.
Now, we understand the basic concepts for the theory of Red-Black Trees, which can examine the properties and algorithm mechanism of this data structure.
Red-Black Trees
There are several key properties to remember when examining Red-Black Tree data structures, since these properties will constitute which nodes are rotated when new data is inserted into the tree.
Properties:
- The root is black. This is the uppermost node. The rest of the nodes are considered Children of the root.
- Every red node must have two black child nodes.
- A node is either red or black.
- All leaves (NIL) are black. A leaf is a vertex or node which has the degree of 1 (one edge connected to the vertex).
- Every simple path from any given node through it's subsequent leaves contains the same number of black nodes.
Insertion:
For the insertion of new data into the tree, the complexity of this operation is O(log n) for both Average and Worst Case situations. To insert new data into the tree, we must check for a insertion point, which will one of the NIL nodes. Once the insertion point has been found (sentential node), then the new node will be coloured red and the properties of the tree will be checked. The parent node of the newly inserted node will be checked, and recoloured if needed. Rotations on the tree may be performed to validate the other properties of the tree.
Deletion:
The complexity of deletion is again O(log n) for both cases. The deletion of nodes follows a similar process as before.
Space:
The data structure uses very little memory, and has a space complexity of O(n) in both Average and Worst Case.
References:
Sorting and Searching Algorithms - The Cookbook
Red-Black Tree Wikipedia
Graph Theory (Graduate Texts in Mathematics) - Reinhard Diestel
Subscribe to:
Posts (Atom)